啊……

序章 兰伯特问题简介
之前写过两篇文章介绍了开普勒轨道参数与轨道状态的转换,而在天体动力学中还有另一个重要的问题称作兰伯特问题:已知两定点\(\vec r_1, \vec r_2\),求在固定于原点的标准重力参数为\(\mu\)的中心天体引力作用下,小天体或航天器从\(\vec r_1\)出发到达\(\vec r_2\)的转移轨道。
由于开普勒运动肯定是一个平面运动,首先尝试将问题从三维降到二维处理。虽然\(\vec r_1, \vec r_2\)和原点已经唯一确定了转移轨道平面,但这个平面的“正反”还不能确定。换句话说,即使\(\vec r_1, \vec r_2\)已经确定,它们之间的夹角\(\Delta \theta\)仍可能有两个取值:劣角(\(\Delta \theta\lt\pi\))或优角(\(\Delta \theta\ge\pi\))。故此,还需要选定小天体角动量的方向,使得从角动量指向的一侧看去,\(\Delta \theta\)无论优劣都在转移平面中由\(\vec r_1\)逆时针转向\(\vec r_2\),这样\(\Delta \theta\)就可唯一确定。在实际问题中,提前确定角动量的方向也是很有意义的,比如从地球发射航天器到火星,那肯定是希望转移轨道的角动量和地球、火星轨道角动量对齐而不是相反,否则航天器必须进入太阳逆行轨道,\(\Delta v\)爆炸。
二维化后的问题成为:已知平面上两点与中心的距离\(r_1=|\vec r_1|\),\(r_2=|\vec r_2|\);两点间夹角\(\Delta\theta=\angle\vec r_1 O\vec r_2\);以及中心天体的标准重力参数\(\mu\),求经过这两点\(\vec r_1, \vec r_2\)的开普勒轨道。下图给出兰伯特问题的一个示例,展示了\(\Delta\theta\ge\pi\)的情形。图中点\(O\)为中心天体;红线给出一条可行转移轨道,实线是从起点\(\vec r_1\)运动到终点\(\vec r_2\)的弧,虚线是转移不经过的轨道弧:
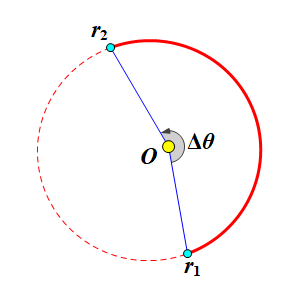
显然,这样的轨道有无数条。但有一个经典的结论:只要\(\Delta\theta\)不超过一圈(\(2\pi\)),那么任意给定一个时间\(\Delta t\gt 0\),就能唯一确定一条开普勒轨道,满足从\(\vec r_1\)出发到达\(\vec r_2\)的耗时为\(\Delta t\)。
这也是兰伯特问题的最终目标:已知\(r_1, r_2, \Delta\theta\),根据给定的\(\Delta t\)求解出轨道。不过,由于\(\Delta t\)的表达式较为复杂,直接从\(\Delta t\)求解轨道参数是非初等的。故一般的做法是引入一个另外的自由参数\(\xi\),使得轨道参数和\(\Delta t\)可同时用关于\(\xi\)的初等函数表达,通过求解方程\(\Delta t=\Delta t(\xi)\)确定出\(\xi\)后再计算结果轨道参数。
这篇文章主要就是介绍我发现的一个新的自由参数\(\xi\),使用这个参数给出的兰伯特问题算法比许多教科书或者其他地方的算法都要简洁许多,基本上所有比较重要的轨道参数(包括轨道角动量、偏心率、始末点速度和始末点的真近点角)以及\(\Delta t\)都能用已知量\(r_1, r_2, \Delta\theta\)和\(\xi\)在一两个公式之内给出。本文不会给出这些公式的详细证明推导(大概),因为太长了(懒)……总之读者可以自行尝试证明或者验证~~~

第一章 轨道参数及转移时间计算
先介绍本文求解所引入的自由参数\(\xi\),其定义为
\[\xi=\left\{\begin{aligned}&\cos\frac{\Delta E}{2}, &e\lt 1\\
&1, &e=1\\
&\cosh\frac{\Delta E}{2}, &e\gt 1
\end{aligned}\right.
\]
其中\(\Delta E=E_2-E_1\)为转移前后偏近点角之差;\(e\)是转移轨道的偏心率。根据转移轨道是椭圆(\(e\lt 1\))、抛物线(\(e=1\))还是双曲线(\(e\gt 1\)),从\(\Delta E\)计算\(\xi\)的方法也有不同。总得来说,\(\xi\)是对这三种轨道普适定义的“偏近点角半差余弦”。显然,按照定义,\(\xi\ge -1\)。
同时还需要定义一个无量纲量\(u\):
\[u=\frac{2\sqrt{r_1 r_2}}{r_1+r_2}\cos\frac{\Delta\theta}{2}\]
显然有\(-1\le u \le 1\);这是仅与兰伯特问题的已知量有关的一个常数,不随\(\xi\)变化。
计算特征速度:
\[v_0=\sqrt{\frac{2\mu}{(r_1+r_2)(1-u\xi)}}\]
则转移轨道的单位质量角动量\(j\)可直接写出:
\[j=v_0\sin\frac{\Delta\theta}{2}\sqrt{r_1 r_2}\]
始末点的径向速度\(v_{r1}, v_{r2}\)、角向速度\(v_{\theta1}, v_{\theta2}\)亦可直接写出:
\[\begin{aligned}
v_{r1}&=v_0\left(\cos\frac{\Delta\theta}{2}\sqrt{\frac{r_2}{r_1}}-\xi\right),\quad
&v_{\theta1}=\frac{j}{r_1}=v_0\sin\frac{\Delta\theta}{2}\sqrt{\frac{r_2}{r_1}}\\
v_{r2}&=v_0\left(\xi-\cos\frac{\Delta\theta}{2}\sqrt{\frac{r_1}{r_2}}\right),\quad
&v_{\theta2}=\frac{j}{r_2}=v_0\sin\frac{\Delta\theta}{2}\sqrt{\frac{r_1}{r_2}}\\
\end{aligned}\]
始末点的真近点角\(\theta_1, \theta_2\)仍可直接写出:
\[\theta_1=\arctan\frac{-2\xi\sin\frac{\Delta\theta}{2}\sqrt{r_1 r_2}+r_2\sin\Delta\theta}{2\xi\cos\frac{\Delta\theta}{2}\sqrt{r_1 r_2}-r_1-r_2\cos\Delta\theta}\\
\theta_2=\arctan\frac{+2\xi\sin\frac{\Delta\theta}{2}\sqrt{r_1 r_2}-r_1\sin\Delta\theta}{2\xi\cos\frac{\Delta\theta}{2}\sqrt{r_1 r_2}-r_2-r_1\cos\Delta\theta}\]
一以贯之地,这里的\(\arctan\frac{y}{x}\)仍然定义为 \( \arg(x+\mathrm{i}y)\),即二元 \(\arctan\) 函数。此外还需注意,如果转移轨道是正圆,上述真近点角的计算式会成为\(\arctan\frac{0}{0}\)。在正常的编程语言(如c++)中,使用\((0,0)\)调用二元\(\arctan\)函数会给出\(0\)。此时直接使用上述两式分别计算\(\theta_1\)和\(\theta_2\)会给出同样的\(0\)值,这会导致\(\theta_2-\theta_1\neq\Delta\theta\)。实际计算中,圆轨道的近点辐角具体是多少无关紧要,故可仅用上式之一计算始末点之一的真近点角,另一个使用\(\Delta\theta=\theta_2-\theta_1\)得出,这样可以保证从始末点能计算出一致的近点辐角\(\omega=\arg\vec r_1-\theta_1=\arg\vec r_2-\theta_2\)。
继续,轨道的偏心率\(e\)及形状参数\(q\)还是可以直接写出:
\[q=e^2-1=\frac{4r_1r_2(\xi^2-1)\sin^2\frac{\Delta\theta}{2}}{(r_1+r_2)^2(1-u\xi)^2}\]
注意到此时确定转移轨道形状及转移速度所需的所有参数都已给出,且所有公式都是初等、普适、无需分段的。而其他方法如Bate法中,计算这些参数前还需首先计算两个定义复杂的分段初等函数,即Stumpff \(S\)和\(C\)函数,显得复杂许多。
有了上述参数就足以画出转移轨道了。这里给出\(\xi\)取不同值时一些转移轨道的具体示例:
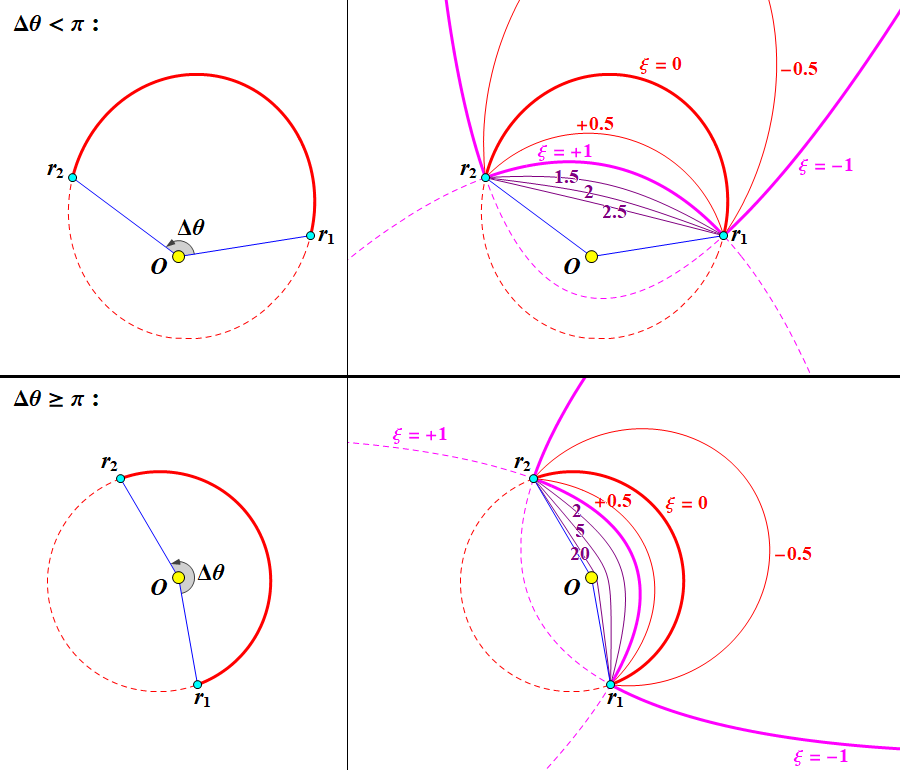
上图上下两行分别给出转移角\(\Delta\theta\lt\pi\)及\(\Delta\theta\ge\pi\)的两种情形,并在右侧给出当自由参数\(\xi\)取不同值时轨道的形状;椭圆轨道用红色标出,抛物线轨道为粉紫色,双曲线轨道为紫罗兰色。右侧图中\(\xi\)取值从其下限\(-1\)开始逐渐增加。当\(\xi=\cos\frac{\Delta E}{2}=-1\)时,转移轨道应为椭圆且偏近点角之差\(\Delta E=2\pi\),这对应高偏心率的椭圆趋于抛物线时的极限轨道:首先前往无限远点,然后从无限远处返回并抵达终点。当\(-1\lt\xi\lt 1\)时,转移轨道为椭圆弧且逐渐收小。当\(\xi=1\)时,转移轨道重新成为抛物线,不过此次是从抛物线的近点侧而非远点侧经过,由于抛物线轨道在有限远处偏近点角恒为\(0\),这对应\(\Delta E=0\)。当\(\xi\gt 1\)继续上升时,转移轨道成为偏心率逐渐增加的双曲线。此时如果\(\Delta\theta\lt\pi\)(即上图中右上子图),则\(u\gt 0\),由于计算轨道参数所用的公式中有\(\sqrt{1-u\xi}\),可知\(\xi\)有上限\(\frac{1}{u}\)。当\(\xi\)接近这一上限时,特征速度\(v_0\)趋于无穷,也即转移轨道趋于以无限大的速度直线前往终点。对\(\Delta\theta\ge\pi\)(即上图中右下子图)的情形,\(\xi\)没有上限。随着\(\xi\)趋于无穷,轨道将趋于从中心天体任意近距离飞掠而过的“折线”。
最后是转移时间,直接写出:
\[\Delta t=\frac{2\mu}{v_0^3}\left(\frac{1+u}{(1+\xi)(1-u\xi)}+\mathrm{kep}~\xi\right)\]
其中\(v_0\)是本章之前定义的特征速度,也与\(\xi\)有关;\(\mathrm{kep}\)是一个分段初等函数,利用它可以简化许多开普勒问题中关于时间和平近点角的计算式,其具体定义可见这篇文章。
在\(\xi\lt 1\),即转移轨道为椭圆时,小天体还可以先绕行中心天体\(n\)整圈之后再经过\(\Delta\theta\)抵达终点。这只影响转移时间\(\Delta t\)的计算,不影响其他轨道参数及轨道速度。此时只需将转移时间中的\(\mathrm{kep}~\xi\)替换为\(\mathrm{kep}_n\xi\)即可,其定义为:
\[\mathrm{kep}_n x=\frac{n\pi+\arccos x}{(1-x^2)^{3/2}}-\frac{1}{1-x^2}\]
当然,在\(n=0\)时,\(\mathrm{kep}_0 x\)就是\(\mathrm{kep}~x\)。下图给出当\(n=0, 1, 2, 3\)时\(\mathrm{kep}_n x\)的图像。可见当\(n=0\)时,\(\mathrm{kep}~x\)在\(x\gt -1\)内是是单调递减的光滑连续函数,但当\(n\gt 0\)时,\(\mathrm{kep}_n x\)仅在\(-1\lt x\lt 1\)内有定义,且先减后增。
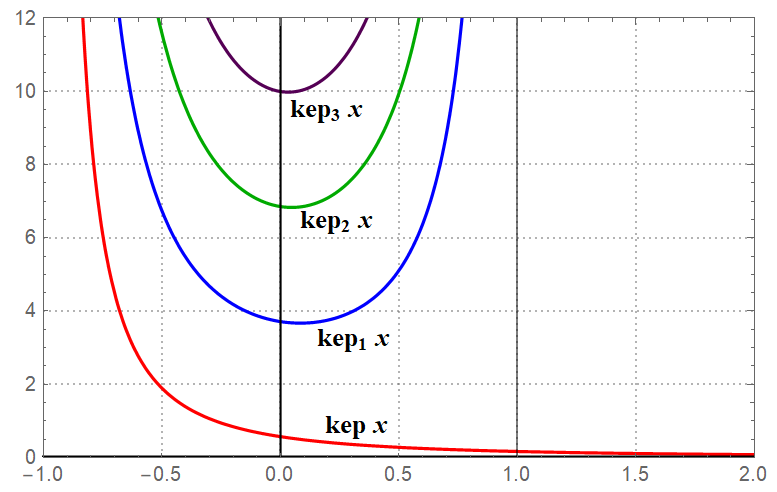
任意给定一个\(\Delta t^*\)后,使用数值方法求解方程\(\Delta t(\xi^*)-\Delta t^*=0\)就能得到转移轨道对应的\(\xi^*\)值,进而求出轨道参数及转移速度。求解一般使用牛顿迭代法,但具体实现中会有许多细节,比如首先要找一个较好的初值;每步迭代时不仅需要计算\(\Delta t(\xi)\)还需要计算其导数\(\Delta t'(\xi)\);以及由于\(\Delta t(\xi)\)的性质并不太好,实际求解中最好是先将其平方,求解方程\(\Delta t^2(\xi^*)-\Delta t^{*2}=0\)。关于这些细节可能会有第二章详细说明,也许吧。
未完待续?
咕咕咕~~~